Zápočtové úlohy

Fyzikální a matematické konstanty deklarujte jako parametry.

Dodržujte zásady strukturovaného programování.

Pokud ve vašem úkolu je generování náhodných čísel použijte na začátku programu příkaz call random_seed(), viz náhodná čísla .

Pokud je součástí vašeho úkolu zobrazení výsledku v grafu, můžete použít jakýkoliv nástrej chcete. Avšak doporučuji použít gnuplot. Ke každému, takovému úkolu je k dispozici gnuplot script. Script se spustí pomocí příkazu v příkazovém řádku

gnuplot -e 'l "nazevScriptu.gpl"'

nebo spuštěním gnuplotu příkazem gnuplot a potom příkazem

l "nazevScriptu.gpl"

nebo i dvojklikem. Scritp lze otevřít v textovém editoru (např. poznámkový blok). U scriptu je nutné změnit jména souborů, které se mají vykreslovat. Ty jsou označeny komentářem, který se ve gnuplotu píše za #. Gnuplot scripty můžete také spouštět automaticky z fortran kódu příkazem

call execute_command_line("gnuplot -e 'l ""nazevScriptu.gpl""'")

K zobrazení můžete také použít webové rozhraní u příslušné úlohy, kde je také ukázka výstupu. V případě nefunkčnosti mi dejte prosím vědět (nejspíš to nebude fungovat v IE). Poslední řádek textového pole nechte prázdný. Upozornění pokud vložíte hodnoty v nesprávném tvaru může dojít k chybě, která se nebude líbit vašemu prohlížečí.

Balení dárku

Naprogramujte program, který spočítý tzv. convexní obal množiny bodů (ve 2D). Jinými slovy nalezněte takové body v množině bodů, které když spojíme úsečkami, tak tím “obalíme” celou množinu. Tato úloha se řeší pomocí algoritmu balení dárku (https://en.wikipedia.org/wiki/Gift_wrapping_algorithm).

Algoritmus funguje následovně:

Z monožiny bodů vyberte bod, který leží nejvíce vlevo - $p_0$ .
Bod $p_{i+1}$ nalezneme tak, že všechny body leží napravo od přímky $p_i p_{i+1}$ .
Algoritmus opakujeme dokud $p_{i+1} = p_0$

https://en.wikipedia.org/wiki/Gift_wrapping_algorithm#/media/File

.gif

Druhý bod realizujeme pomocí měření úhlu mezi vektory $p_i p_{i-1}$ a $p_i p_{i+1}$ . Kde $p_{i+1}$ je takový bod pro který je úhel mezi vektory největší. Pro nalezení bodu $p_1$ uvažujme, že vektor $p_i p_{i-1} = (0.0, -1.0)$ .

Množinu bodů nagenerujte náhodně např. jen na intervalu $(0,1) \times (0,1)$ .

Počet bodů deklarujte jako parameter.

Pro nalezení bodu $p_{i+1}$ napište funkci nebo subroutinu.

Množinu bodů zapište do souboru ve formátu “x y”, kde x a y jsou souřadnice bodů. Viz ukázka.

Výsledný obal množiny zapište do souboru ve formátu “x y”, kde x a y jsou souřadnice bodů, které tvoří obal. Viz ukázka.

Pseudo kód:

generuj mnozinu bodu
najdi bod obalu p_0
najdi bod obalu p_1
dokud se p_0 nerovná p_i+1
	spocitej uhly mezi vektory (p_i, p_*), (p_i, p_i-1)
	p_i+1 = p_* s nejmenším úhlem

vypis vsechny body
vypis body tvorici obal

Správnost řešení si ověřte vykreslením výsledku do grafu. ( gnuplot script )

Růst sněhové vločky

Simulujte proces růstu struktury podobné sněhové vločce. Uvažujte čtvercovou mřížku. Na Náhodnou pozici této mřížky položte částici. V každém kroku tuto částici posuňte na náhodný sousední uzel mřížky. Pohyb částice se zastaví ve chvíli kdy částice narazí na jinou částici resp. ve chvíli kdy částice sousedí s jinou částicí. Potom vygenerujte další částici na náhodnou pozici a proces opakujte. Pokud se částice dostane do nějaké větší vzdálenosti, zapomeňte na ni a vygenerujte novou. Na počátu umistěte 3x3 částic do středu soustavy.

https://en.wikipedia.org/wiki/Diffusion-limited_aggregation

Praktická realizace je taková, že budete mít 2D pole reprezentující mřížku ve kterém bude uložena informace kde je usídlena částice a kde ne.

Pojem sousední uzel se dá chápat dvěma způsoby boď jako 4 uzli po stranách nebo jako 8 uzlu (postranách a rohy). Volbu kterou definici sousedních uzlů použijete je na vás.

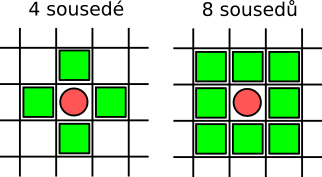
Pozici pohybující se částice reprezentujte jako dva integery nebo 2D pole integeru.

Pro testování zda pohybující se částice má v okolí jinou částici napište funkci nebo subroutinu.

Pro náhodné posunutí napište funkci nebo subroutinu.

Větu “Pokud se částice dostane do nějaké větší vzdálenosti” chápejme tak, že částice se ocitne mimo pole.

Růst vločky ukončete ve chvíli kdy se usadilo určené množství částic.

Výsledek zapište do souboru ve formátu “x y”, kde x a y jsou polohy usazených částic. Viz ukázka.

Pole doporučuji deklarovat ve tvaru (-n:n,-n,n), ale je to na vás.

Pseudo kód:

nastavit pole na počateční hodnotu
nastavit střed pole 3x3 prvků na hodnotu indikující usazenou částici
dokud není usazeno N částic
	vygeneruj počáteční polohu pohybujícíse částice
	dokud v okolí pohybující se částine není usídlená částice
		posuň částici do náhodného sousedního uzlu
	
vypiš polohy usazených částic

Pro ověření správnosti zobrazte výsledek v grafu. ( gnuplot script )

Gaussova eliminační metoda

Napište program, který bude řešit soustavu lineárních rovnic pomocí Gaussovy eliminační metody (https://cs.wikipedia.org/wiki/Gaussova_elimina%C4%8Dn%C3%AD_metoda). Program bude mít následující procedury: nacti, spocitej, vypis. Procedura “nacti” načte ze souboru matici ve formátu:

n
a11 a12 ... a1n b1
...
an1 an2 ... ann bn

Kde n je velikost matice. Po načtení n naalokujte velikost polí.

Procedura “spocitej” vyřeší soustavu pomocí gaussovy eliminační metody.

Procedura “vypis” vypíše výsledek na obrazovku a do souboru.

U metody se může vyskytnout problém pokud bude na diagonále 0. Uvažujte jen matice, kde na diagonále žádná nula není. Případ kdy je na diagonále 0 nemusíte nijak ošetřovat. Také předpokládejte lineární nezávislost všech rovnic.

Pseudo kód:

procedura spocitej
cyklus přes sloupce, i-tý - sloupec
	cyklus přes řádky, j-tý - řádek
		od j-tého řádku odečteme takové číslo aby A(i,j) = 0

cyklus přes řádky k, od posledniho k prvnímu
dopočítej x(k)

Příklady vstupních souboru: soustava 1 , soustava 2 , soustava 3 . Příklady obsahují kromě zadání také správná řešení.

Numerická integrace

Napište dvě procedury, které spočítají určitý integrál funkce na zadaném intervalu. Jedna procedura bude počítat integrál lichoběžníkovou metodou a druhá metodou Monte Carlo.

Procedury budou mít jako argumenty hodnoty a, b, funkci f(x) a parametry metody.

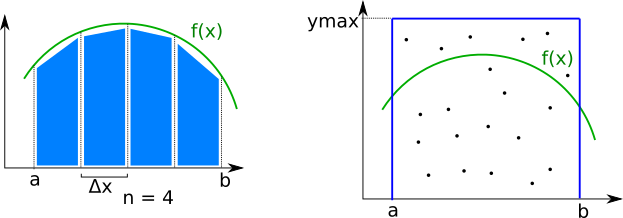
Lichoběžníková metoda počítá plochu pod křivkou tak, že interval $<a,b>$ rozdělí na $n$ dílků o šířce $\Delta x = \frac{b - a}{n}$ . Obsah každého dílku aproximuje jako lichoběžník s plochou $\frac{f(x_i)+f(x_{i+1})}{2} \Delta x$ . Integrál získáme sečtením všech lichoběžníků. Je zřejmé že čím větší $n$ , tím je vetší přesnost metody. $n$ bude parametrem procedury

Metodou Monte Carlo se integruje pomocí generování náhodných čísel. Uvažme toto: Funkci $f(x)$ ohraničíme obdelníkem o stranách $(b-a)$ a $y_{max}$ . $y_{max}$ představuje hodnotu která je na celém intervalu $< a,b >$ větší než maximum funkce $f(x)$ . Potom pravděpodobnost, že námi vygenerovaný náhodný bod v ohraničujícím obdelníku bude vygenerován pod funkci $f(x)$ je roven poměru obsahu plochy pod křivkou (tedy integrálu $f(x)$ ) ku ploše obdelníku ( $S_{f(x)}/S_{obdelnik}$ ). Pravděpodobnost získáte tak, že budete generovat velké množství bodů do obdelníku a počítat kolik z nich spadlo pod křivku $f(x)$ . Pravděpodobnost je potom dána vzorcem $p = \frac{N_{pod f(x)}}{N_{celkove}}$ , kde $p$ je pravděpodobnost, $N_{pod f(x)}$ je počet bodů vygenerovaných pod křivku $f(x)$ a $N_{celkove}$ je počet všech vygenerovaných bodů. Integrál je potom $I = p \cdot S_{obdelnik}$ . Parametry této medoty budou $y_{max}$ a $N_{celkovy}$ .

Použíjte obě metody na stejnou funkci a stejný interval a výsledky vypište do souboru.

Předpokládejme, že funkce nabývá hodnot >0. Jinak by bylo třeba používat také $y_{min}$

Funkci f(x) napište jako funkci a metodám se bude předávat jako argument.

Ověřte si analytický výpočtem správnost výsledků. (např. na https://www.wolframalpha.com/)

Pseudo kód monte carlo:

cyklus N_celkove -krát
	vygeneruj náhodný bod (xp,yp) v obdelníku (a,b)X(0, y_max)
	pokud yp < f(xp)
		pricti k N_pod_f(x) +1
konec cyklu
spocitej pravdepodobnost
spocitej integral

Hledání klastrů

Proveďte klastrovou analýzu množiny bodů. Na počátku vygenerujte náhodně množinu bodů např. jen do čtverce na intervalu $(0,1)\times(0,1)$ . Klastrová analýza znamená, že nalezneme podmnožiny bodů, které jsou od ostatních odděleny, v tomto případě nějakou vzdáleností $d_{max}$ , tj. hledáme skupiny bodů. $d_{max}$ je maximální vzdálenost mezi dvěma body, aby spolu byli ve skupině .

Pro analýzu potřebujeme 3 pole. Jedno ve kterém bude uloženo v jakém klastru se bod nacházi, $kb$ . Druhé které nám bude říkaz kolik bodů je v jakém klastru $nk$ . Třetí které nám bude říkat jaký bod je v jakém klastru (bude dvourozměrné), $klastry$ .

Na počátku nastavíme, že každý bod je ve svém vlastním klatru o velikosti jedna.

Následně postupně měříme vzdálenosti mezi všemi páry a pokud je vzdálenost mezi body menší naž $d_{max}$ , tak všechny body z klastru druhé částice nastavíme jako body klastru první částice.

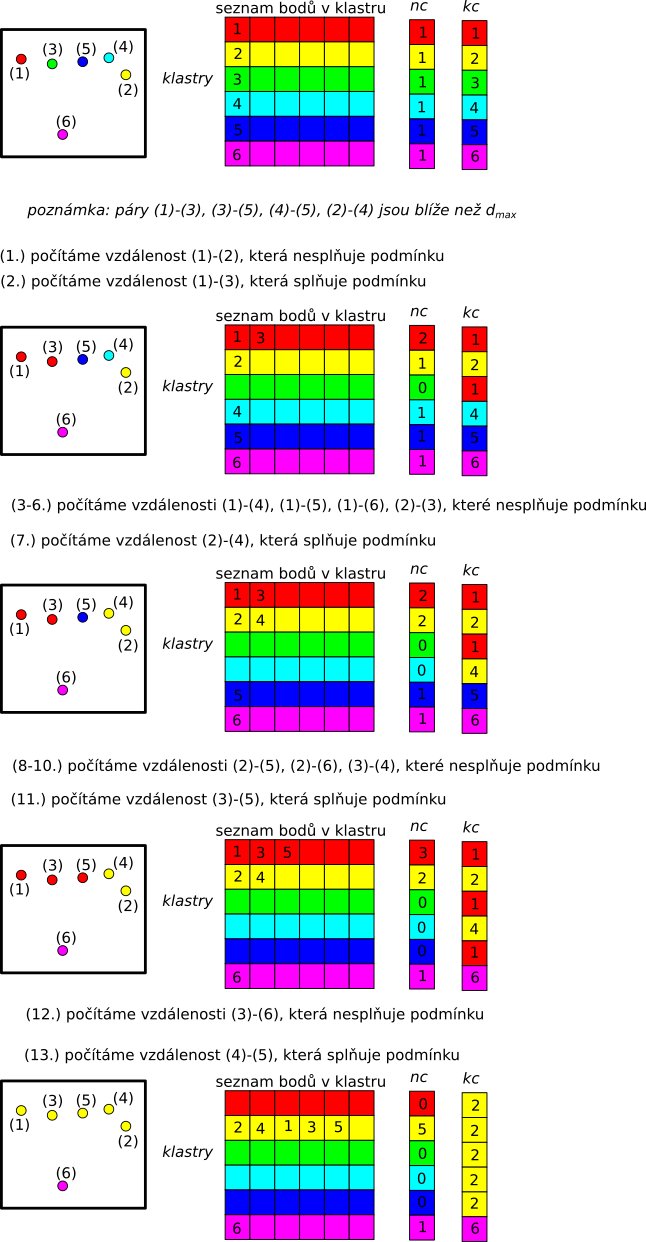
vygeneruj N bodů
nastav kb na [1, 2, 3, ..., N]
nastav všechny hodnoty v nc na 1
nastav první sloupeček klastry na [1, 2, 3, ..., N]
cyklu i jde od 1 do N
	cyklus j jde od 1 do N, j/=i
		spočítej vzdálenost d mezi bodem i a j
		pokud d < d_max
			přidej všechny body z klastru j do klastru bodu i

vypis klastry

Rozumná hodnota $d_{max}$ závisí na počtu částic. Pro $N = 100$ je rozumné $d_{max} = 0.1$

Pro přidání bodů z jednoho klastru do druhého napište funkci nebo subroutinu.

Výsledné klastry vypište do souboru v následujícím formátu:

x_11	y_11
x_12	y_12
...

x_21 y_21
x_22 y_22
...

x_11 znamená x souřadníce bodu 1 v klastru 1, x_12 znamená x souřadníce bodu 2 v klastru 1, atd. Viz ukázka.

Pro vizuální kontrolu si výsledek vykreslete do grafu. ( gnuplot script )

Monte Carlo minimalizace

Mějme $N$ náhodně rozmístěných bodů ve čtverci $L \times L$ . Pomocí metody Monte Carlo zařiďte, aby body byly rozmístěny po čtverci co nejrovnoměrněji.

Metoda Monte Carlo je metoda založená na náhodě. V každém kroku posunete jeden bod náhodným směrem o nějaký malý krok. Tuto novou konfiguraci příjmete pokud bude splněna vhodná podmínka. V našem případě bychom měli konfiguci přijmout pokud bude systém v “uspořádanějším” stavu.

Charakterizovat uspořádanost nemusí být lehké, ale uspořádaný systém bude nejspíš takový, kde si body od sebe drží rozestupy. Zaveďme tedy váhovou funkci, která bude záviset na vzdálenosti bodů.

u(r_{ij}) = \frac{1}{r_{ij}}

, kde

r_{ij}

je vzdálenost mezi body (tzn. velikost vektoru

\vec r_{ij}

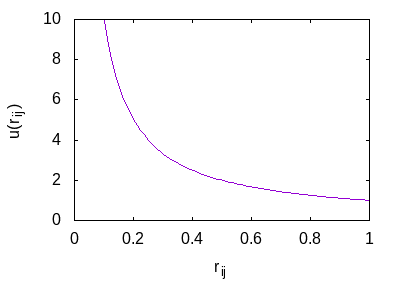
Pokud budou u sebe dva body blízko bude váha tohoto páru větší než když budou dál. Celkovou váhu bodu $i$ můžeme spočátat jako $U_i = \sum_{j=1, j\neq i}^N u(r_{ij})$ .

Když se pokusíme posunout jednu částici, tak její novou polohu příjmeme pokud se její váha zmenší.

Malý krok $dr$ bude parametrem a doporučuji jej zvolit příbližně $L/100$

Celkový počet iterací $N_{iteraci}$ je dalším parametrem a závisí zejména na $dr$ a $L$ . Volba $N_{iteraci} = 1000$ by měla stačit.

Pro výpočet váhy bodu $i$ napište funkci nebo subroutinu.

Pro vygenerování náhodného posunutí bodu napište funkci nebo subroutinu.

Počáteční rozložení bodů zapište do souboru ve formátu “x y”, kde x a y jsou polohy bodů. Viz ukázka.

Konečné (uspořádané) rozložení bodů zapište do souboru ve formátu “x y”, kde x a y jsou polohy bodů. Viz ukázka.

Pseudo kód:

vygeneruj N bodů do náhodných pozic ve čtverce LxL
cyklus N_iteraci -krát
	cyklus přes všechny body, i jde od 1 do N
		spocitej váhu bodu i vaha
		zkus posunout bod i náhodným směrem o dr
		spocitej váhu posunutého bodu i vaha_test
		pokud vaha_test < vaha
			přijmi posunutí bodu i

Správnost výsledku si ověřte vykreslením obou konfigurací do grafu. ( gnuplot script )

Hledání nejkratší cesty

Pomocí Dijkstrova algoritmu nalezněte nejkratší cestu z jednoho rohu čtvercové mřížky $(1,N) \times (1,N)$ do protilehlého rohu. Na mřížce uvažujte překážku umístěnou tak, aby nejkratší cesta nebyla po diagonále.

Dijkstrův algoritmus je algoritmus na hledání nejkratší cesty v grafu. Náš graf je čtvercová mřížky. Začínáme v bodě (1,1) a chceme se dostat do bodu (N,N) nejkratší cestou. Pohybovat se můžeme do stran i do diagonálních směrů. Algoritmus funguje tak, že systematicky navštěvujeme všechny buňky a počítáme jejich vzdálenost od buňky (1,1).

https://cs.wikipedia.org/wiki/Dijkstr%C5%AFv_algoritmus

Budete potřebovat tři pole. V jednom poli bude uložena informace o tom zda jsme toto pole již navštívili. V druhém poli bude informace o tom jak daleko se nachází od pozice (1,1). Také budeme potřebovat pole pro reprezentování překážek.

Na počátku budou všechny buňky kromě bodu (1,1) nastaveny jako nenavštívená a vzdálenost k nim bude nastavena na největší možnou velikost (teoreticky nekonečno, prakticky huge(…)). Jen bodu (1,1) nastavíme vzdálenost 0.

Pokaždé když označíme bod mřížky jako navštívený můžeme dopočítat vzdálenost k jeho dosud nenavštíveným sousedním bodům. Pokud je tato vzdálenost menší než je jeho současná hodnota, nastavíme tuto vzdálenost jako jeho novou hodnotu.

V každém kroku algoritmu nastavíme jeden bod jako navštívený a to takový který jsme ještě nenavštívili a má nejmenší vzdálenost.

Tuto část algoritmu opakujeme dokud nenavštívíme bod (N,N).

pozn. na obrázku je hodnota buňek vzdálenost od (1,1). Zelená barva indikuje, že buňka již byla navštívena.

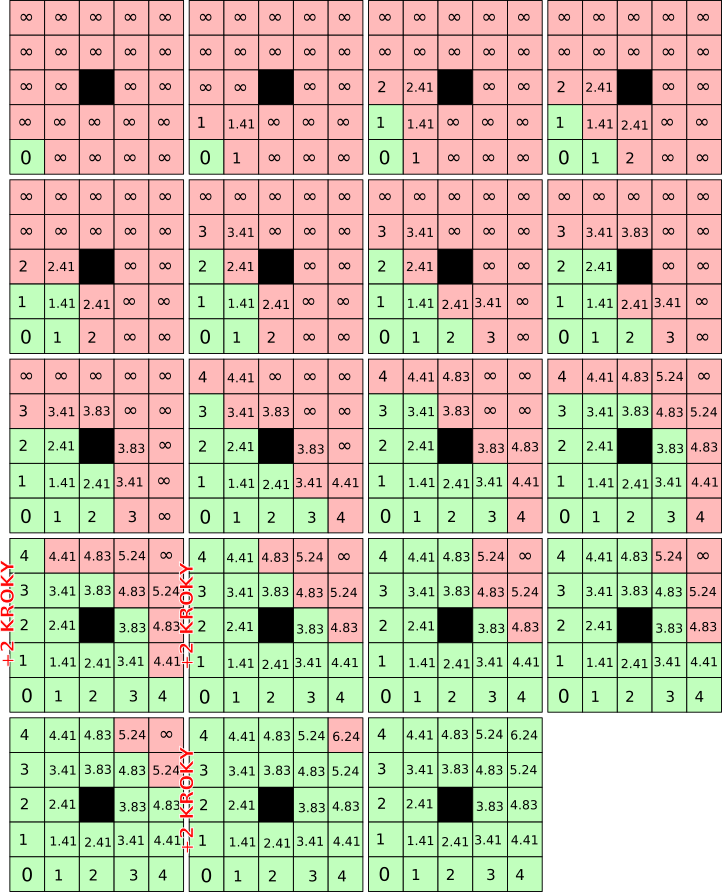
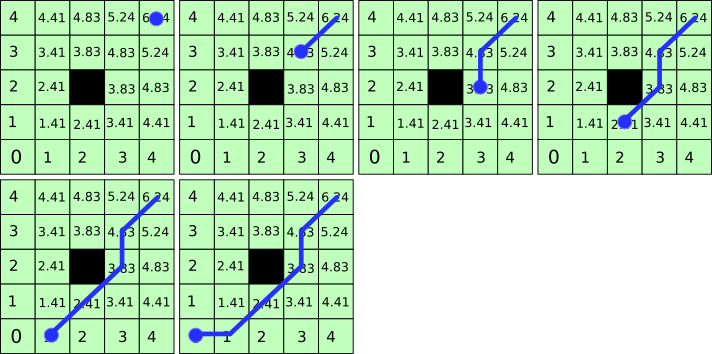
Když jsou všechny podstatné body mřížky označeny vzdáleností. Můžeme nalézt nejkratší cestu tak, že začneme v bodě (N,N) a půjdeme zpět do bodu (1,1). Přičemž pokaždé se posuneme do sousedního bodu s nejmenší hodnotou. Řešení nemusí být pouze jedno, ale všechna jsou stejně dobrá, tak nezáleží na tom které zvolíme.

Pro spočítání vzdáleností sousedních buněk napište funkci nebo subroutinu.

Pro nalezení nenavštívené buňky s nejmenší vzdáleností napište funkci nebo subroutinu.

Pseudo kód:

nastav pole vzdáleností, d = huge, jen d(1,1) = 0
nastav pole s překážkami p
nastav pole indikujicí navštívení n na false, jen n(1,1) = true
spocitej vzdálenosti do sousedních buněk buňky (1,1)
dokud n(N,N) /= true
	najdi bunku (kx, ky) s n=false, p=false a zároveň nejmenším d
	spocitej vzdálenosti sousedních buněk z buňky (kx,ky)
	pokud je tato vzdálenost menší než je její současdé d
		nastav d na menší hodnotu

nastav polohu p_0 na (N,N)
dokud p_i /= (1,1)
p_i = sousedni bunka p_i-1 s nejmenší hodnotou

Polohy přákážek vypište do souboru ve formátu “x y”, kde x a y jsou polohy uzlů s překážkami. Viz ukázka.

Seznam uzlů tvořících nejkratší cestu zapište do souboru ve formátu “x y”, kde x a y jsou polohy uzlů, tak jak jdou popořadě. Viz ukázka.

Správnost výsledku si ověřte vykreslením výsledků do grafu. ( gnuplot script )

Řadící algoritmy

Seřaďte hodnoty v poli od nejmenšího po největší pomocí algoritmu a) bubble sort b) merge sort.

Na počátku do pole o velikosti $N$ nagenerujte náhodné hodnoty.

Pro bubble sort potřebujete jednu logickou proměnnou, která bude indikovat zda jste provedli změnu nebo ne. Postupně testujeme všechny sousední dvojce v poli tj. zda $p_{i} > p_{i+1}$ . V případě, že podmínka platí, tyto prvky prohodíme a logickou proměnnou nastavíme na stav indikující, že jsme udělali změnu. Na začátku každého cyklu logickou proměnnou nastavíme na stav “žádná změna”. Celý algoritmus opakujeme dokud po dokončení celého cyklu nezůstane logická proměnná ve stavu “žádná změna”.

Zde je bubble sort velmi dobře vysvětlený: https://cs.wikipedia.org/wiki/Bublinkov%C3%A9_%C5%99azen%C3%AD

Merge sort je rekurzivní algoritmus pracující ve dvou fázích. Nejprve rozdělíme pole na dvě poloviny a setřídíme každou zvlášť (zde je ta rekurze). Tyto dvě poloviny následně spojíme. Spojení polí probíhá tak, že vezmeme první hodnoty každého z polí a do výsledného pole přídáme tu menší. Zároveň tu hodnotu kterou jsme přidali z původního pole odebereme. Takto pokračujeme dokud není jedno s polí prázdné. Potom zbytek druhého pole přidáme nakonec výsledného pole.

https://cs.wikipedia.org/wiki/Merge_sort

Každou metodu napište jako funkci nebo subroutinu.

Pseudo kód merge sortu:

funkce mergeSort(pole)
	pokud velikost pole == 1
		výsledek = pole
	jinak
		střed = velikost pole / 2
		cast_1 = mergeSort( pole (1 : střed) )
		cast_2 = mergeSort( pole (střed+1 : velikost pole) )
		výsledek = spoj(cast_1 , cast_2)

funkce spoj(cast_1 , cast_2)
dokud velikost cast_1 > 0 a velikost cast_2 > 0
pokud prvni prvek cast_1 <= prvni prvek cast_2
přidej první prvek cast_1 do výsledek
odeber první prvek z cast_1
jinak
přidej prvni prvek cast_2 do výsledek
odeber první prvek z cast_2

    pokud velikost cast_1 > 0
    	pridej zbytek pole cast_1 do výsledek

    pokud velikost cast_2 > 0
    	pridej zbytek pole cast_2 do výsledek

pozn. Tento pseudokód ilustruje pouze myšlenku která se skrývá za algoritmem. Fortran nemá možnost takto přímočaře pracovat s poli.

Setříděné pole vypište do souboru. Na 1 řádek 1 hodnotu. Viz ukázka.

Správnost výsledku si ověřte vykreslením výsledků do grafu. ( gnuplot script )

Problém obchodního cestujícího - nejbližší sousedé

Řešte metodou nejbližších sousedů problém obchodního cestujícího.

Problém ochodního cestujícího je optimalizační problém, kdy je úkolem naléz nejkratší možnou trasu mezi všemi městy na mapě, tak abychom každé město navštívili pouze jednou.

Tento problém je při výpočtu hrubou silou (tj. spočítat všechny možné variace) pro větší počet měst neřešitelný, neboť počet možností je dán $N!$ . Proto se pro řešení tohoto problému používají různá zjednodušení, které nemusí vždy nalézt nejlepší řešení, ale snaží se k němu přiblížit.

Pro popis problému budeme potřebovat pole ve kterém budou polohy měst. Dále pole integerů ve kterém bude uloženo pořadí měst, tak jak by se měla navštívit.

Polohy měst nastavte na náhodné hodnoty.

Metoda nejbližších sousedů funguje tak, že na počátku vybereme jedno z měst (např. to první). Pro toto město najdeme nejbližší město a k němu se vydáme. Pro toto město najdeme znovu nejbližší, zatím nenavštívené město, atd. Algoritmus ukončíme po navštívení všech měst.

Tento postup rozšiřte tak, že postupně zkusíte zvolit každé město jako počáteční. Z těchto tras vyberte jako výsledek tu nejkratší.

Pro výpočet vzdáleností napište funkci nebo proceduru.

Polohy měst, tak jak by se měla navštívit vypište do souboru ve formátu “x y”, kde x a y jsou polohy měst. Viz ukázka.

Pseudo kód:

vygeneruj náhodně polohy N mest
poradi = [1 , ...]
dokud nenavstivime vsechna mesta, i jde od 2 do N
	spocitej vzdalenost mesta i-1 se vsemi dosud nenavstivenymi mesty
	poradi(i) = mesto s nejmenší vzdáleností

Správnost výsledku si ověřte vykreslením výsledků do grafu. ( gnuplot script )

Problém obchodního cestujícího - simulované žíhání

Řešte metodou simulovaného žíhání problém obchodního cestujícího.

Problém ochodního cestujícího je optimalizační problém, kdy je úkolem naléz nejkratší možnou trasu mezi všemi městy na mapě, tak abychom každé město navštívili pouze jednou.

Pro popis problému budeme potřebovat pole ve kterém budou polohy měst. Dále pole integerů ve kterém bude uloženo pořadí měst, tak jak by se měla navštívit. Na počátku bude toto pole jen (1, 2, 3, …, N).

Polohy měst vygenerujte náhodně na počátku programu.

Pro realizaci algoritmu potřebujeme nastavit počáteční “teplotu” systému, $T$ , a nějaké číslo $K$ , které bude charakterizovat “rychlost ochlazování”. V každém kroku nastavíme $T = T \cdot K$ .

Na počátku spočítáme aktuální délku cesty. V každém kroku vybereme náhodně dvě města a spočítáme jaká by byla délka cesty kdybychom jejich pořadí prohodili. To zda pořadí měst prohodíme nebo ne rozhodneme pomocí Metropolisova algoritmu. Ten udává, že pravděpodobnost přijetí nového uspořádání v případě, že $d_{nove}>d_{soucasne}$ je

P = \exp \left( \frac{-(d_{nove}-d_{soucasne})}{T} \right)

, kde

d

jsou délky cest. V opačném případě (

P_{nove}<P_{soucasne}

) je

P = 1

. To znamená, že pokud by nová cesta byla lepší přijmeme ji vždy a také, že s jistou pravděpodobností můžeme přijmout horší cestu.

Prakticky se algoritmus realizuje tak, že vygenerujeme náhodné číslo $u \in (0,1)$ . A pokud $u <= \exp \left( \frac{-(d_{nove}-d_{soucasne})}{Teplota} \right)$ , tak nové pořadí přijmeme.

Dalším důležitým parametrem algoritmu je počet iterací $N_{iteraci}$ tj. kolikrát se pokusíme změnit pořadí měst. Nebojte se toho, když algoritmus poběží pro 100 měst pár sekund. Klidně nastavte počet iterací na několik miliónů.

Pro výpočet délky trasy napište funkci nebo subroutinu.

Hodnotu počáteční $T$ volte příbližně v intervalu (1, 100). Hodnotu $K$ ve tvaru 0.999…, tak aby neklesala příliš rychle ani pomalu vzhledem k počtu iterací. Mě se osvědčili tyto dvě sady parametrů pro 100 měst: (1) $N_{iteraci}=10000000$ , $T=10$ , $K=0.999999$ ; (b) $N_{iteraci}=1000000$ , $T=10$ , $K=0.99999$ . Varianta (b) je rychlejší, proto se hodí pro první testy, ovšem dává horší výsledek.

Polohy měst, tak jak by se měla navštívit vypište do souboru ve formátu “x y”, kde x a y jsou polohy měst. Viz ukázka.

Pseudo kód:

vygeneruj náhodně polohy N mest
poradi = [1, 2, 3, ... N]
spočitej délku trasy d
nastav T
nastav K
dokud neproběhne N_iteraci
	vygeneruj dvě náhodná integer čísla i1, i2
	spočítej délku trasy d_test pokud by si města i1 a i2 prohodili poradí navštívení &
					tj. prohod poradi(i1) <=> poradi(i2) 
	vygeneruj náhodné číslo u s rovnoměrným rozdělením na intervalu (0,1)
	pokud u<=exp(-(d_test-d)/T)
		poradi = pořadí s prohozeným pořadím měst i1 a i2
		d = d_test

    T = K * T

Správnost výsledku si ověřte vykreslením výsledků do grafu. ( gnuplot script )

Simulace Sluneční soustavy

Napište program, který načte ze souboru hmotnosti, polohy a rychlosti planet. Následně spustí jejich simulaci. Uvažujte případ, kdy planety jsou v jedné rovině (2D). Slunce umístěte do počátku souřadnic a nastavte nulovou rychlost.

První řádek vstupního souboru bude počet planet $n$ a na dalších $n$ řádcích budou postupně hmotnosti, polohy a rychlosti těles ve formátu “m x y vx vy”, kde m je hmotnost; x, y sou souřadnice a vx, vy jsou složky vektoru rychlosti.

Po načtení $n$ teprve naalokujte potřebná pole.

Pro počáteční polohy je vhodné použít hodnoty velkých poloos (wikipedia). Pro počáteční rychlost hodnoty průměrných rychlostí (wikipedia). Dejte si pozor na jednotky!

Vzhledem k velkým číslům použijte dvojitou přesnost (tj. real(8)).

Pro simulaci pohybu použijte metodu ARV z http://fyzikalniolympiada.cz/texty/modelov0.pdf - část 2.

Časový krok zvolte přibližně 1000s.

Pro výpočet síly popř. zrychlení napište funkci nebo subroutinu.

Nasimulujte alespoň 1 rok.

Polohy těles zapisujte pravidelně do souboru ve formátu “čas x_1 y_1 x_2 y_2 x_3 y_3 …”, viz ukázka. Polohy těles stačí zapisovat každých např. 100 kroků, ale záleží na vás.

Správnost výsledku si ověřte vykreslením výsledků do grafu. ( gnuplot script )

Pseudo kód:

nacti n těles ze souboru
dokud neuplyne správný čas
	spočítej zrychlení
	spočítej nové polohy
	spočítej nové rychlosti

Problém stabilních manželství

https://en.wikipedia.org/wiki/Stable_marriage_problem

Řešte problém stabilních manželství pomocí Gale-Shapley algoritmu.

Problém stabilních manželství je následující: Máme dvě sady objektů, A a B. Obě sady jsou stejně velké. Naším úkolem je uspořádat je do dvojic tak, že každý můžeme být součástí jen jedné dvojice. Každý objekt má seznamem druhé sady objektů seřazený, podle preferencí.

Dvojice je nestabilní pokud jeden ze členů má na seznamu preferencí výše někoho z jiného páru než současného partnera a ten má zárověň na seznamu výše jeho než svého současného partnera. Problém jsme vyřešili pokud neexistují nestabilní páry.

V algoritmu je jedna sada objektů žádající a drůhá čekající na nabídku. Uvažujme že A budou žádat a B budou čekat na nabídky. Páry budeme hledat do té doby dokud nebudou všechna A zadány. V každém kroku budou postupně všechna nezadaná A nabízet partnerství takovému B, které je nejvýše na jejich seznamu a kterého se zatím naptali.

Pokud dotazované B je volné nebo jeho současný partner je na jeho seznamu umístěn hůře než tan který žádá, příjme nové partnerství a jeho současný partner se stává nezadaným.

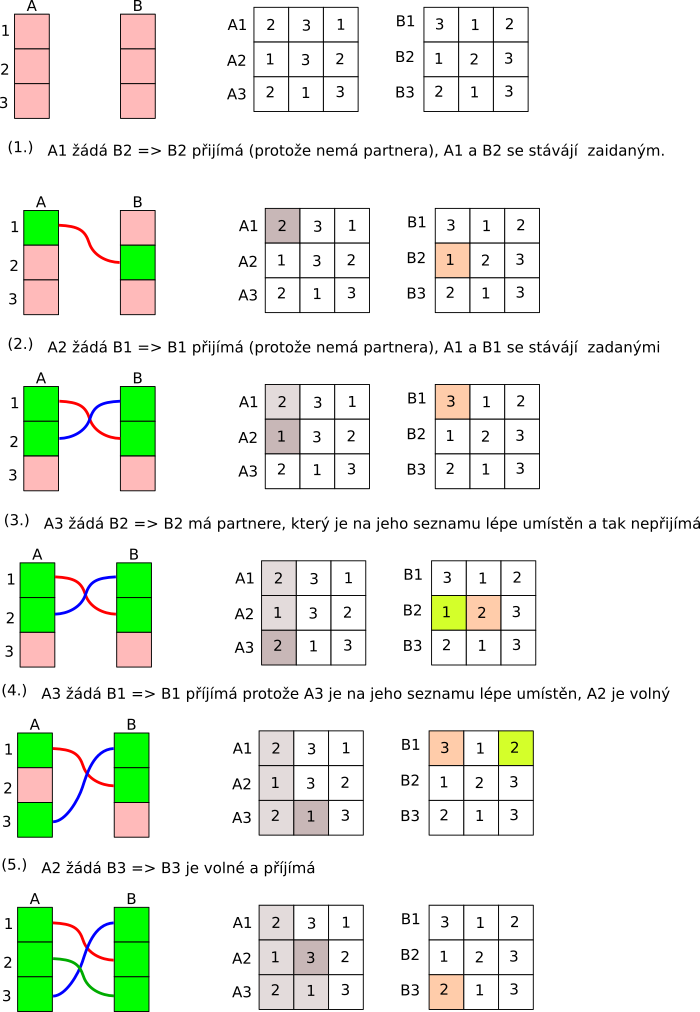
Pro náhodné generování seznamů preferencí můžete použít následující modul generovaniAB_mod.f90 . Používá se pomocí call generujAB(n, A, B), kde n je velikost seznamů, A a B jsou pele ve tvaru A(n,n), B(n,n). První index určuje prvek z množiny (A ,B) a druhým indexem se prochází seznam preferencí. Např. A(1,:) je seznam prefenrencí prvního prvku A.

Pro vyhodnocení žádosti napište funkci nebo subroutinu.

Pseudo kód:

nacti seznam preferenci pro všechna A a B
nastav všechna A a B na nezadané
dokud nejsou všichni zadáni
	cyklus přes všechna A, i jde od 1 do N
		pokud je A_i nezadané
			žádá dálší B na svém seznamu, které zatím nežádal
		pokud je žádané B volné nebo A_i je na jeho seznamu lépe &
															umístěn než současný partner
			partner žádaného B se stává nezadaný
			A_i a žádané B tvoří pár

vypiš všechny páry

Problém výběru aktivit

https://cs.wikipedia.org/wiki/Probl%C3%A9m_v%C3%BDb%C4%9Bru_aktivit

Řešte problém výběru aktivit pomocí hladové metody.

Problém výběru aktivit spočívá v nalezení největšího množství nepřekrývajících se aktivit.

Na počátku máme množinu aktivit s intervaly od kdy do kdy tato aktivita může probíhat. Cílem je vabrat takové, abychom jich stihli co nejvíce.

První krok je seřadit aktivity primárně podle koncového času a sekundárně podle času začátku aktivity.

Následně vybereme první aktivitu v seznamu.

Další aktivitu vybereme takovou, která nezačíná dříve než předchozí končí.

Na počátku vygenerujte N aktivit s náhodným časem začátku a náhodnou délkou. Čas začátku generujte jako integer od 8 do 18 a délku od 1 do 3.

Pro třídění aktivit napiště funkci nebo soubroutinu s metodou bubble sort. Zde je bubble sort velmi dobře vysvětlený: https://cs.wikipedia.org/wiki/Bublinkov%C3%A9_%C5%99azen%C3%AD

Nakonec vypište (1) seznam všech aktivit tj. jejich časy začátku a konce, (2) výsledný seznam vybraných aktivit. Výpis proveďtě na obrazovku a do souboru. Výpis všech aktivit a vybraných aktivit oddělte mezerou.

Pseudo kód:

vygeneruj N aktivit
setřiď aktivity primárně podle času konce a sekundárně podle času začátku
přidej první aktivitu do výběru
cyklu přes seznam aktivit
	pokud aktivita začíná potom co předchozí zkončila
		přidej aktivitu do výběru

vypiš všechny aktivity
vypiš výběr aktivit

Řešení polynomu do 3. řádu

Napište program, který řeší polynom do 3. řádu (a) analyticky a (b) přibližným řešením pomocí metody půlení intervalu.

Rovnici uvažujte ve tvaru $a x^3 + b x^2 + c x + d = 0$ .

https://cs.wikipedia.org/wiki/Kubick%C3%A1_rovnice

Zdroj pro analytické řešení: http://physics.ujep.cz/~mlisal/fortran/quadratic_cubic_eqs.pdf

Koeficienty a, b, c, d načtěte z klávesnice nebo ze souboru.

Řešení ošetřete pro případ, že a=0 (řešíte kvadratickou rovnici); a=0 a b=0 (řešíte lineární rovnici).

Metoda půlení intervalů: https://cs.wikipedia.org/wiki/P%C5%AFlen%C3%AD_interval%C5%AF

Tato metoda je určena k nalezení 1 kořene. Vstupem metody je interval $(a,b)$ ve kterém se nachází jeden kořen rovnice. Potom platí, že $f(a) \cdot f(b) < 0$ , neboť jedno z $f(a)$ nebo $f(b)$ je vždy záporné a jedno kladné. Metoda je iterativní, to znamená, že se postupně přibližuje ke správnému řešení. V každé iteraci spočítáme $f(p) = f(\frac{a+b}{2})$ . Pokud je např. $f(p) \cdot f(b) < 0$ , tak to znamená, že kořen se nalézá na intervalu $(p,b)$ jinak na intervalu $(a,p)$ . V dalším kroku používá tento nový interval. Čím větší počet iterací, tím přesnější řešení.

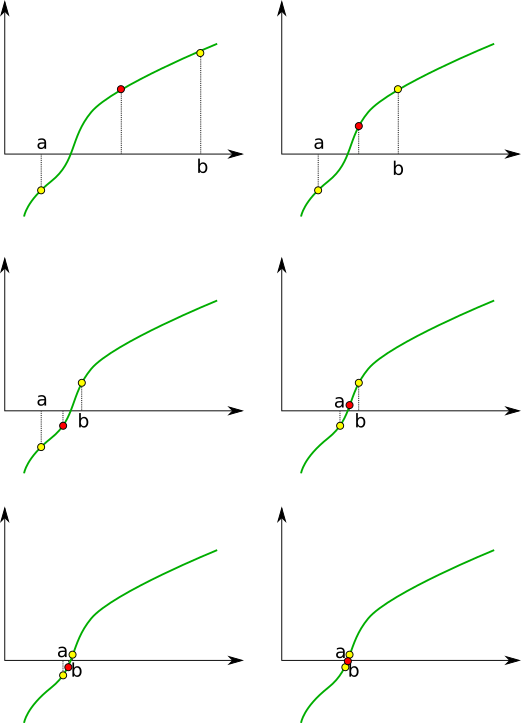
Metodu půlení intervalu rozšiřte pro nalezení všech kořenů na intervalu $(a,b)$ . Rozšíření bude následující: Rozdělte interval $(a,b)$ na $N$ dílků o šířce $\Delta x = \frac{b - a}{N}$ . Každý tento dílek otestujte zda $f(x_i) \cdot f(x_{i+1}) < 0$ , kde $x_i$ a $x_{i+1}$ jsou krajní polohy dílku. Pokud je podmínka splněna, znamená to, že se v daném intervalu nalézá kořen. Na každý takový dílek použijte metodu půlení intervalu.

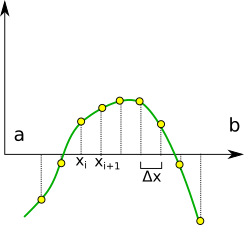
Pro řešení kvadratické rovnice analyticky napište funkci nebo subroutinu.

Pro řešení kubické rovnice analyticky napište funkci nebo subroutinu.

Metodu půlení intervalu napište jako funkci nebo subroutine.

Medotou půlení intervalu hledejte pouze reálné kořeny.

Nalezená řešení vždy vypište na obrazovku a do souboru.

Pseudo kód půlení intervalů:

procedura puleni intervalu (a,b)
cyklu do požadovaného počtu iterací
	spocitej střed intervalu p = (a+b)/2
	pokud f(p)*f(a) < 0
		b = p
	jinak
		a = p

Příklady rovnic:

$x^2 - x - 6 =0$ => [x1=3, x2=-2]
$x^2 - 4x + 4 = 0$ => [x1=x2=2]
$x^2 - 2x + 5 = 0$ => [x1=1+i2, x2=1-i2]
$x^3 - 11x^2 + 36x - 36 = 0$ => [x1=6, x2=3, x3=2]